掌握标准差计算技巧：轻松理解数据离散程度的核心指标

当我们谈论一组数据时，比如一个班级的考试成绩、一家公司员工的月薪，或者一周内每天的气温，我们常常会用一个“平均数”来概括它们的整体水平，平均数确实很有用，它能告诉我们数据的中心点在哪里，它有一个很大的局限：它无法告诉我们数据是紧密地围绕在这个中心点周围,还是分散得七零八落。

想象两个班级，数学期末考试的平均分都是80分，甲班级的成绩是78, 79, 80, 81, 82；而乙班级的成绩是60, 70, 80, 90, 100，虽然平均分相同，但这两个班级的情况天差地别，甲班级的学生水平非常整齐，大家考得都差不多；而乙班级的学生则两极分化严重，既有高分也有低分，这个时候，我们就需要一个指标来衡量这种“离散程度”或“波动性”，而标准差就是干这个用的，标准差就是用来衡量一组数据到底有多“散”的一把尺子，标准差小，说明数据点都紧紧抱团在平均值附近；标准差大，说明数据点各自为政,离平均值比较远。

这把“尺子”是怎么做出来的呢？它的计算过程其实非常有逻辑，我们可以一步步来拆解，完全不用害怕那些看起来复杂的公式，根据统计学家帕尔·图利在《统计学》中的阐述,计算标准差通常分为以下几个步骤：

第一步，计算平均数，这个大家都会，就是把所有数据加起来，然后除以数据的个数,这是我们衡量离散程度的基准点。

第二步，计算每个数据点与平均数的“差距”，具体做法是，用每一个数据减去第一步算出来的平均数，这个差距可能是正数（数据比平均大），也可能是负数（数据比平均小），比如在乙班级，平均分80分，90分的差距是+10，60分的差距是-20。

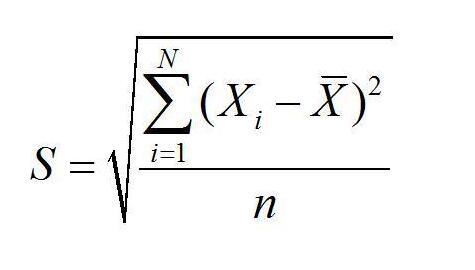
第三步，把所有的“差距”平方，为什么要平方呢？主要有两个原因：一是为了消除正负号的影响，因为无论是+10还是-10，平方后都变成100，这样我们就可以把所有差距都当作正数来处理；二是平方会放大那些距离平均值较远的点的影响，使得标准差对异常值更加敏感,这通常是我们希望看到的。

第四步，计算这些“平方差距”的平均数，把所有第二步平方后得到的数值加起来，再除以数据的个数（如果计算的是样本标准差，则除以n-1，这里我们暂且按总体标准差来理解，除以n），这一步得到的结果叫做“方差”，方差已经能代表离散程度了，但它的单位是原始数据的平方，比如如果原始数据是“分”，方差就是“分的平方”,这不太好理解。

第五步，开平方，对第四步得到的方差开平方根，这样就把它变回了原始数据的单位，这个最终的结果,就是标准差！

我们再用乙班级的例子（60, 70, 80, 90, 100）来简单演算一下：

1. 平均数 = (60+70+80+90+100)/5 = 80。
2. 计算差距：60-80=-20，70-80=-10，80-80=0，90-80=10，100-80=20。
3. 平方差距：(-20)²=400，(-10)²=100，0²=0，10²=100，20²=400。
4. 求平方差距的平均数（方差）：(400+100+0+100+400)/5 = 1000/5 = 200。
5. 开平方：√200 ≈ 14.14。

乙班级成绩的标准差大约是14.14分，这意味着，大部分学生的成绩分布在平均分80分上下14.14分的范围内，作为对比，你可以自己算一下甲班级（78, 79, 80, 81, 82）的标准差，会发现它非常小，可能只有1.4左右,直观地反映了成绩的集中程度。

理解了计算过程，我们就能更好地应用它，在投资中，标准差是衡量风险的关键指标，标准差大的股票，意味着价格波动剧烈，风险高，在产品质量控制中，标准差小意味着生产流程稳定，产品质量均匀，在教育测评中，标准差可以帮助老师分析试卷的区分度，正如道格拉斯·W·哈伯德在《数据化决策》中指出的，认识到数据的变异性（即离散程度）是做出明智决策的第一步,而标准差是量化这种变异性的最常用工具。

标准差不是一个神秘莫测的数学符号，它源于一个非常直观的想法：看看每个数据离平均值有多远，然后综合起来得到一个代表性的距离，掌握了这个核心思路，你就能轻松地理解和运用标准差,让它成为你解读数据世界的有力助手。