探索不同形状面积计算方法：从基础到精通的实用指南

好,咱们来聊聊面积这事儿吧，其实一开始 我觉得面积计算有啥好说的，不就是长乘宽嘛，小学就学过了，但后来发现，这事儿越想越有意思，甚至有点…哲学？比如你看着一个圆，它明明这么光滑，怎么就能用πr²这么一个带小数点的数给框住呢？这本身就很神奇。

先从最规矩的说起,长方形，这大概是所有人的起点，长乘宽，简单直接，我小时候还干过傻事，拿尺子量家里的茶几，量完长和宽，乘起来得到一个数，然后就觉得，哇，我掌握了这片玻璃的大小！好像拥有了它的一部分似的，但这种喜悦很快就被三角形打破了，为什么是底乘高除以二？当时老师用两个一样的三角形拼成一个平行四边形来解释，我表面上懂了，心里却嘀咕：那要是找不到另一个一模一样的三角形咋办？这种不完整的思考伴随了我很久，直到后来才明白，公式背后是严密的逻辑，但当时那种半懂不懂的纠结，现在想起来还挺真实的。

然后说到平行四边形,它的面积是底乘高，我第一次意识到“高”不一定在图形里边，比如一个歪着的平行四边形，它的高得从外面垂下来量，这让我觉得，数学有时候也挺“狡猾”的，它不总是你看上去的样子，你得透过现象看本质… 高，是一种垂直的距离，跟它站不站在图形里头没关系，这种概念的延伸，算是第一个小门槛。

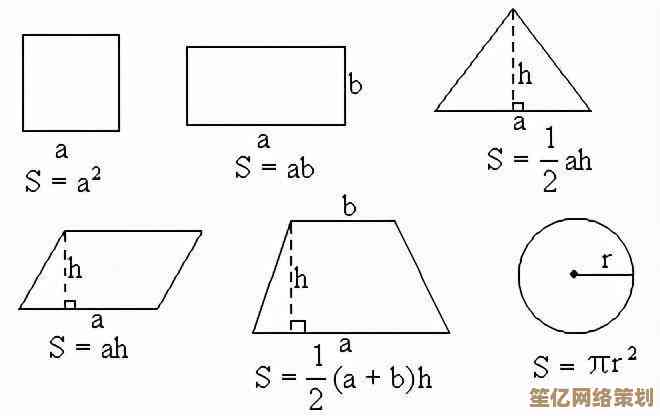
接着是梯形,上底加下底的和乘高除以二，这个公式我老是记混顺序，有时候会写成（上底乘高 + 下底乘高）除以二，虽然结果一样，但显得我思路很绕，教我的那位老师脾气有点急，看我这么写就会皱眉头，但我自己觉得，用自己的方式推导出来，哪怕绕点路，也比死记硬背强，对吧？学习的过程不就是允许自己走点弯路嘛。

圆,绝对是面积计算里的一个“大明星”，也最让人头疼。π 这个无限不循环小数，本身就带着一种神秘感，你永远算不尽它，我记得第一次用公式算圆的面积时，看着计算器上那一长串数字，感觉特别不真实，我们居然用一个永远不完整的数，去定义了一个完整的、封闭的形状，这种矛盾感，让我第一次觉得数学不仅仅是工具，它也在描述一种界限，一种我们无限逼近却无法完全抵达的完美，后来我还试过把圆剪成很多小扇形，拼成一个近似的长方形，那种亲手“转化”的过程，比光看公式印象深多了，虽然拼得歪歪扭扭，但那个“哦，原来是这样！”的瞬间，比什么都值。

再往后,遇到那些不规则的形状，事情就更有趣了，比如一片树叶的面积怎么算？这时候公式没用了，我试过最笨的方法，把它画在方格纸上，数格子，大于半格算一个，小于半格舍去… 数得眼花缭乱，结果当然是个大概齐，但这种“近似”的感觉，反而更贴近生活，生活中哪有什么绝对的精确呢？都是个估计，这种方法虽然原始，却有一种亲手摸索的踏实感。

说到精通,我觉得不是说你背熟了所有公式，而是你能感觉到公式之间的联系，你会发现三角形的公式和平行四边形的有关，梯形的公式好像能涵盖长方形… 它们不是一个孤岛，有时候闲着没事，我会在纸上画图，试着把一种图形转化成另一种，去验证它们的面积关系，这种自己探索出来的“发现”，比书上直接告诉你的要印象深刻一百倍。

这本“指南”如果真的有用，可能不在于它列出了多少公式，而在于它能不能勾起你那种“自己动手试试看”的冲动，拿起纸笔，画一画，剪一剪，甚至去量量你房间地板的面积… 在那种有点混乱、充满个人痕迹的摸索里，那些冰冷的公式才会真正活过来，变成你自己的东西，面积计算，说到底，是我们理解世界大小和空间的一种方式，而理解的方式，本来就可以很自由，很个人化。